
The goal of grasps is to provide a collection of statistical methods that incorporate both element-wise and group-wise penalties to estimate a precision matrix, making them user-friendly and useful for researchers and practitioners.
\[\hat{\Omega}(\lambda,\alpha,\gamma) = {\arg\min}_{\Omega \succ 0} \{ -\log\det(\Omega) + \text{tr}(S\Omega) + \lambda P_{\alpha,\gamma}(\Omega) \},\]
\[P_{\alpha,\gamma}(\Omega) = \alpha P^\text{idv}_\gamma(\Omega) + (1-\alpha) P^\text{grp}_\gamma(\Omega),\]
\[P^\text{idv}_\gamma(\Omega) = \sum_{i,j} p_\gamma(\vert\omega_{ij}\vert),\]
\[P^\text{grp}_\gamma(\Omega) = \sum_{g,g^\prime} p_\gamma(\Vert\Omega_{gg^\prime}\Vert_F).\]
For more details, see the vignette Penalized Precision Matrix Estimation in grasps.
The package grasps provides functions to estimate precision matrices using the following penalties:
| Penalty | Reference |
|---|---|
Lasso
(penalty = "lasso") |
Tibshirani (1996); Friedman et al. (2008) |
Adaptive lasso
(penalty = "adapt") |
Zou (2006); Fan et al. (2009) |
Atan (penalty = "atan") |
Wang and Zhu (2016) |
Exp (penalty = "exp") |
Wang et al. (2018) |
Lq (penalty = "lq") |
Frank and Friedman (1993); Fu (1998); Fan and Li (2001) |
LSP (penalty = "lsp") |
Candès et al. (2008) |
MCP (penalty = "mcp") |
Zhang (2010) |
SCAD (penalty = "scad") |
Fan and Li (2001); Fan et al. (2009) |
See the vignette Penalized Precision Matrix Estimation in grasps for more details.
You can install the development version of grasps from GitHub with:
# install.packages("devtools")
devtools::install_github("Carol-seven/grasps")library(grasps)
## reproducibility for everything
set.seed(1234)
## block-structured precision matrix based on SBM
sim <- gen_prec_sbm(d = 30, K = 3,
within.prob = 0.25, between.prob = 0.05,
weight.dists = list("gamma", "unif"),
weight.paras = list(c(shape = 20, rate = 10),
c(min = 0, max = 5)),
cond.target = 100)
## synthetic data
library(MASS)
X <- mvrnorm(n = 20, mu = rep(0, 30), Sigma = sim$Sigma)
## solution
res <- grasps(X = X, membership = sim$membership, penalty = "adapt", crit = "HBIC")
## visualization
plot(res)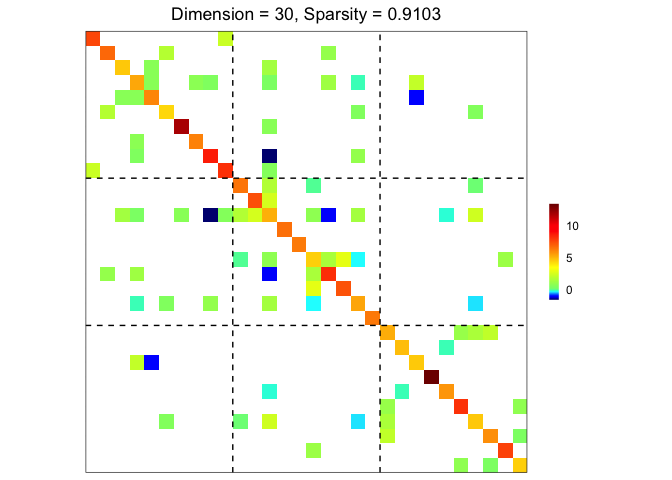
## performance
performance(hatOmega = res$hatOmega, Omega = sim$Omega)
#> measure value
#> 1 sparsity 0.9103
#> 2 Frobenius 24.6796
#> 3 KL 7.2063
#> 4 quadratic 54.1949
#> 5 spectral 13.1336
#> 6 TP 22.0000
#> 7 TN 370.0000
#> 8 FP 17.0000
#> 9 FN 26.0000
#> 10 TPR 0.4583
#> 11 FPR 0.0439
#> 12 F1 0.5057
#> 13 MCC 0.4545