Type:	Package
Title:	Solving Mixed Model Equations in R
Version:	4.4.4
Date:	2025-11-19
Maintainer:	Giovanny Covarrubias-Pazaran <cova_ruber@live.com.mx>
Description:	Structural multivariate-univariate linear mixed model solver for estimation of multiple random effects with unknown variance-covariance structures (e.g., heterogeneous and unstructured) and known covariance among levels of random effects (e.g., pedigree and genomic relationship matrices) (Covarrubias-Pazaran, 2016 <doi:10.1371/journal.pone.0156744>; Maier et al., 2015 <doi:10.1016/j.ajhg.2014.12.006>; Jensen et al., 1997). REML estimates can be obtained using the Direct-Inversion Newton-Raphson and Direct-Inversion Average Information algorithms for the problems r x r (r being the number of records) or using the Henderson-based average information algorithm for the problem c x c (c being the number of coefficients to estimate). Spatial models can also be fitted using the two-dimensional spline functionality available.
Depends:	R (≥ 3.5.0), Matrix (≥ 1.1.1), methods, stats, MASS, crayon, enhancer
LazyLoad:	yes
License:	GPL-2 | GPL-3 [expanded from: GPL (≥ 2)]
Imports:	Rcpp (≥ 0.12.19)
BugReports:	https://github.com/covaruber/sommer/issues
URL:	https://github.com/covaruber/sommer
LinkingTo:	Rcpp, RcppArmadillo, RcppProgress
Suggests:	rmarkdown, knitr, plyr, parallel, orthopolynom, RSpectra, lattice, testthat (≥ 3.0.0)
VignetteBuilder:	knitr
Config/testthat/edition:	3
NeedsCompilation:	yes
Packaged:	2025-11-19 16:16:34 UTC; giovannycovarrubias
Author:	Giovanny Covarrubias-Pazaran [aut, cre]
Repository:	CRAN
Date/Publication:	2025-11-26 06:20:07 UTC

Additive relationship matrix

Description

Calculates the realized additive relationship matrix. Currently is the C++ implementation of van Raden (2008).

Usage

A.mat(X,min.MAF=0,return.imputed=FALSE)

Arguments

Details

For vanraden method: the marker matrix is centered by subtracting column means M= X - ms where ms is the coumn means. Then A=M M'/c, where c = \sum_k{d_k}/k, the mean value of the diagonal values of the M M' portion.

Value

If return.imputed = FALSE, the n \times n additive relationship matrix is returned.

If return.imputed = TRUE, the function returns a list containing

$A

the A matrix

$X

the imputed marker matrix

References

Endelman, J.B., and J.-L. Jannink. 2012. Shrinkage estimation of the realized relationship matrix. G3:Genes, Genomes, Genetics. 2:1405-1413. doi: 10.1534/g3.112.004259

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Examples

####=========================================####
#### random population of 200 lines with 1000 markers
####=========================================####
X <- matrix(rep(0,200*1000),200,1000)
for (i in 1:200) {
  X[i,] <- ifelse(runif(1000)<0.5,-1,1)
}

A <- A.mat(X)

####=========================================####
#### take a look at the Genomic relationship matrix 
#### (just a small part)
####=========================================####
# colfunc <- colorRampPalette(c("steelblue4","springgreen","yellow"))
# hv <- heatmap(A[1:15,1:15], col = colfunc(100),Colv = "Rowv")
# str(hv)

Autocorrelation matrix of order 1.

Description

Creates an autocorrelation matrix of order one with parameters specified.

Usage

AR1(x,rho=0.25)

Arguments

Details

Specially useful for constructing covariance structures for rows and ranges to capture better the spatial variation trends in the field. The rho value is assumed fixed and values of the variance component will be optimized through REML.

Value

If everything is defined correctly the function returns:

$nn

the correlation matrix

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Examples

x <- 1:4
R1 <- AR1(x,rho=.25)
image(R1)

data(DT_sleepstudy, package="enhancer")
DT <- DT_sleepstudy
head(DT)

# define the correlation between Days
D = with(DT, AR1(Days, rho=0.5))
subs = unique(DT$Subject)
# define the correlation between Subjects
S = diag(length(subs))
rownames(S) <- colnames(S) <- subs
# make the kronecker product
DS = kronecker(D,S, make.dimnames = TRUE)
# form the covariance matrix between units 
# this is assumes correlation between timepoints
DT$ds <- paste(DT$Days, DT$Subject, sep=":")
DS <- DS[DT$ds, DT$ds]
colnames(DS) <- rownames(DS) <- paste0("u",1:nrow(DS))
# fit the residual model
head(DT)

fm2 <- mmes(Reaction ~ Days,
            random= ~ Subject, 
            rcov = ~vsm(ism(units), Gu=DS), # equivalent to Subject:ar1(Days)
            data=DT, tolParInv = 1e-6, verbose = FALSE)
summary(fm2)$varcomp

# the matrix D can take any form: AR1, ARMA, or a custom correlation matrix

Autocorrelation Moving average.

Description

Creates an ARMA matrix of order one with parameters specified.

Usage

ARMA(x, rho=0.25, lambda=0.25)

Arguments

Details

Specially useful for constructing covariance structures for rows and ranges to capture better the spatial variation trends in the field. The rho value is assumed fixed and values of the variance component will be optimized through REML.

Value

If everything is defined correctly the function returns:

$nn

the correlation matrix

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Examples

x <- 1:4
R1 <- ARMA(x,rho=.25,lambda=0.2)
image(R1)

Compound symmetry matrix

Description

Creates a compound symmetry matrix with parameters specified.

Usage

CS(x, rho=0.25)

Arguments

Details

Specially useful for constructing covariance structures for rows and ranges to capture better the spatial variation trends in the field. The rho value is assumed fixed and values of the variance component will be optimized through REML.

Value

If everything is defined correctly the function returns:

$nn

the correlation matrix

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Examples

x <- 1:4
R1 <- CS(x,rho=.25)
image(R1)

Dominance relationship matrix

Description

C++ implementation of the dominance matrix. Calculates the realized dominance relationship matrix. Can help to increase the prediction accuracy when 2 conditions are met; 1) The trait has intermediate to high heritability, 2) The population contains a big number of individuals that are half or full sibs (HS & FS).

Usage

D.mat(X,nishio=TRUE,min.MAF=0,return.imputed=FALSE)

Arguments

Details

The additive marker coefficients will be used to compute dominance coefficients as: Xd = 1-abs(X) for diploids.

For nishio method: the marker matrix is centered by subtracting column means M= Xd - ms where ms is the column means. Then A=M M'/c, where c = 2 \sum_k {p_k (1-p_k)}.

For su method: the marker matrix is normalized by subtracting row means M= Xd - 2pq where 2pq is the product of allele frequencies times 2. Then A=M M'/c, where c = 2 \sum_k {2pq_k (1-2pq_k)}.

Value

If return.imputed = FALSE, the n \times n additive relationship matrix is returned.

If return.imputed = TRUE, the function returns a list containing

$D

the D matrix

$imputed

the imputed marker matrix

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Nishio M and Satoh M. 2014. Including Dominance Effects in the Genomic BLUP Method for Genomic Evaluation. Plos One 9(1), doi:10.1371/journal.pone.0085792

Su G, Christensen OF, Ostersen T, Henryon M, Lund MS. 2012. Estimating Additive and Non-Additive Genetic Variances and Predicting Genetic Merits Using Genome-Wide Dense Single Nucleotide Polymorphism Markers. PLoS ONE 7(9): e45293. doi:10.1371/journal.pone.0045293

Examples

####=========================================####
#### EXAMPLE 1
####=========================================####
####random population of 200 lines with 1000 markers
X <- matrix(rep(0,200*1000),200,1000)
for (i in 1:200) {
  X[i,] <- sample(c(-1,0,0,1), size=1000, replace=TRUE)
}

D <- D.mat(X)

Epistatic relationship matrix

Description

Calculates the realized epistatic relationship matrix of second order (additive x additive, additive x dominance, or dominance x dominance) using hadamard products with the C++ Armadillo library.

Usage

E.mat(X,nishio=TRUE,type="A#A",min.MAF=0.02)

Arguments

Details

it is computed as the Hadamard product of the epistatic relationship matrix; E=A#A, E=A#D, E=D#D.

Value

The epistatic relationship matrix is returned.

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Endelman, J.B., and J.-L. Jannink. 2012. Shrinkage estimation of the realized relationship matrix. G3:Genes, Genomes, Genetics. 2:1405-1413. doi: 10.1534/g3.112.004259

Nishio M and Satoh M. 2014. Including Dominance Effects in the Genomic BLUP Method for Genomic Evaluation. Plos One 9(1), doi:10.1371/journal.pone.0085792

Su G, Christensen OF, Ostersen T, Henryon M, Lund MS. 2012. Estimating Additive and Non-Additive Genetic Variances and Predicting Genetic Merits Using Genome-Wide Dense Single Nucleotide Polymorphism Markers. PLoS ONE 7(9): e45293. doi:10.1371/journal.pone.0045293

Examples

####=========================================####
####random population of 200 lines with 1000 markers
####=========================================####
X <- matrix(rep(0,200*1000),200,1000)
for (i in 1:200) {
  X[i,] <- sample(c(-1,0,0,1), size=1000, replace=TRUE)
}

E <- E.mat(X, type="A#A") 
# if heterozygote markers are present can be used "A#D" or "D#D"

Genome wide association study analysis

Description

THIS FUNCTION IS DEPRECATED. Fits a multivariate/univariate linear mixed model GWAS by likelihood methods (REML), see the Details section below. It uses the mmer function and its core coded in C++ using the Armadillo library to optimize dense matrix operations common in the derect-inversion algorithms. After the model fit extracts the inverse of the phenotypic variance matrix to perform the association test for the "p" markers. Please check the Details section (Model enabled) if you have any issue with making the function run.

The sommer package is updated on CRAN every 3-months due to CRAN policies but you can find the latest source at https://github.com/covaruber/sommer . This can be easily installed typing the following in the R console:

library(devtools)

install_github("covaruber/sommer")

This is recommended since bugs fixes will be immediately available in the GitHub source. For tutorials on how to perform different analysis with sommer please look at the vignettes by typing in the terminal:

vignette("v1.sommer.quick.start")

vignette("v2.sommer.changes.and.faqs")

vignette("v3.sommer.qg")

vignette("v4.sommer.gxe")

or visit https://covaruber.github.io

Usage

GWAS(fixed, random, rcov, data, weights, W,
    nIters=20, tolParConvLL = 1e-03, tolParInv = 1e-06, 
    init=NULL, constraints=NULL,method="NR", 
    getPEV=TRUE,naMethodX="exclude",
    naMethodY="exclude",returnParam=FALSE, 
    dateWarning=TRUE,date.warning=TRUE,verbose=FALSE,
    stepWeight=NULL, emWeight=NULL,
    M=NULL, gTerm=NULL, n.PC = 0, min.MAF = 0.05, 
    P3D = TRUE)

Arguments

Details

Citation

Type citation("sommer") to know how to cite the sommer package in your publications.

Models Enabled

For details about the models enabled and more information about the covariance structures please check the help page of the package (sommer). In general the GWAS model implemented in sommer to obtain marker effect is a generalized linear model of the form:

b = (X'V-X)X'V-y

with X = ZMi

where: b is the marker effect (dimensions 1 x mt) y is the response variable (univariate or multivariate) (dimensions 1 x nt) V- is the inverse of the phenotypic variance matrix (dimensions nt x nt) Z is the incidence matrix for the random effect selected (gTerm argument) to perform the GWAS (dimensions nt x ut) Mi is the ith column of the marker matrix (M argument) (dimensions u x m)

for t traits, n observations, m markers and u levels of the random effect. Depending if P3D is TRUE or FALSE the V- matrix will be calculated once and used for all marker tests (P3D=TRUE) or estimated through REML for each marker (P3D=FALSE).

vignette('sommer.start')

Bug report and contact

If you have any technical questions or suggestions please post it in https://stackoverflow.com or https://stats.stackexchange.com.

If you have any bug report please go to https://github.com/covaruber/sommer or send me an email to address it asap.

Value

If all parameters are correctly indicated the program will return a list with the following information:

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G. Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 2016, 11(6): doi:10.1371/journal.pone.0156744

Covarrubias-Pazaran G. 2018. Software update: Moving the R package sommer to multivariate mixed models for genome-assisted prediction. doi: https://doi.org/10.1101/354639

Bernardo Rex. 2010. Breeding for quantitative traits in plants. Second edition. Stemma Press. 390 pp.

Gilmour et al. 1995. Average Information REML: An efficient algorithm for variance parameter estimation in linear mixed models. Biometrics 51(4):1440-1450.

Kang et al. 2008. Efficient control of population structure in model organism association mapping. Genetics 178:1709-1723.

Lee, D.-J., Durban, M., and Eilers, P.H.C. (2013). Efficient two-dimensional smoothing with P-spline ANOVA mixed models and nested bases. Computational Statistics and Data Analysis, 61, 22 - 37.

Lee et al. 2015. MTG2: An efficient algorithm for multivariate linear mixed model analysis based on genomic information. Cold Spring Harbor. doi: http://dx.doi.org/10.1101/027201.

Maier et al. 2015. Joint analysis of psychiatric disorders increases accuracy of risk prediction for schizophrenia, bipolar disorder, and major depressive disorder. Am J Hum Genet; 96(2):283-294.

Rodriguez-Alvarez, Maria Xose, et al. Correcting for spatial heterogeneity in plant breeding experiments with P-splines. Spatial Statistics 23 (2018): 52-71.

Searle. 1993. Applying the EM algorithm to calculating ML and REML estimates of variance components. Paper invited for the 1993 American Statistical Association Meeting, San Francisco.

Yu et al. 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Genetics 38:203-208.

Tunnicliffe W. 1989. On the use of marginal likelihood in time series model estimation. JRSS 51(1):15-27.

Zhang et al. 2010. Mixed linear model approach adapted for genome-wide association studies. Nat. Genet. 42:355-360.

Examples

####=========================================####
#### For CRAN time limitations most lines in the 
#### examples are silenced with one '#' mark, 
#### remove them and run the examples using
#### command + shift + C |OR| control + shift + C
####=========================================####
#####========================================####
##### potato example
#####========================================####
# 
# data(DT_polyploid, package="enhancer")
# DT <- DT_polyploid
# GT <- GT_polyploid
# MP <- MP_polyploid
# ####=========================================####
# ####### convert markers to numeric format
# ####=========================================####
# numo <- atcg1234(data=GT, ploidy=4);
# numo$M[1:5,1:5];
# numo$ref.allele[,1:5]
# 
# ###=========================================####
# ###### plants with both genotypes and phenotypes
# ###=========================================####
# common <- intersect(DT$Name,rownames(numo$M))
# 
# ###=========================================####
# ### get the markers and phenotypes for such inds
# ###=========================================####
# marks <- numo$M[common,]; marks[1:5,1:5]
# DT2 <- DT[match(common,DT$Name),];
# DT2 <- as.data.frame(DT2)
# DT2[1:5,]
# 
# ###=========================================####
# ###### Additive relationship matrix, specify ploidy
# ###=========================================####
# A <- A.mat(marks)
# ###=========================================####
# ### run it as GWAS model
# ###=========================================####
# ans2 <- GWAS(tuber_shape~1,
#              random=~vsr(Name,Gu=A),
#              rcov=~units,
#              gTerm = "u:Name",
#              M=marks, data=DT2)
# plot(ans2$scores[,1])

Combined relationship matrix H

Description

Given a matrix A and a matrix G returns a H matrix with the C++ Armadillo library.

Usage

H.mat(A, G, tau = 1, omega = 1, tolparinv=1e-6)

Arguments

Details

See references

Value

H Matrix with the relationship between the individuals based on pedigree and corrected by molecular information

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Martini, J. W., Schrauf, M. F., Garcia-Baccino, C. A., Pimentel, E. C., Munilla, S., Rogberg-Munoz, A., ... & Simianer, H. (2018). The effect of the H-1 scaling factors tau and omega on the structure of H in the single-step procedure. Genetics Selection Evolution, 50(1), 16.

Examples

####=========================================####
####random population of 200 lines with 1000 markers
####=========================================####
M <- matrix(rep(0,200*1000),200,1000)
for (i in 1:200) {
  M[i,] <- sample(c(-1,0,0,1), size=1000, replace=TRUE)
}
rownames(M) <- 1:nrow(M)
v <- sample(1:nrow(M),100)
M2 <- M[v,]

A <- A.mat(M) # assume this is a pedigree-based matrix for the sake of example
G <- A.mat(M2)

H <- H.mat(A,G)
# colfunc <- colorRampPalette(c("steelblue4","springgreen","yellow"))
# hv <- heatmap(H[1:15,1:15], col = colfunc(100),Colv = "Rowv")

Multivariate Newton-Raphson algorithm

Description

Multivariate Newton-Raphson algorithm used behind mmes when the henderson argument is set to FALSE. Algorithm made available for users that want to avoid the user-friendly interface and provide their matrices directly.

Usage

MNR(Y, # response
    X, Gx, # fixed effects
    Z, K, # random effects
    R,  # residual effects
    Ge, GeI, # initial values and constraints
    W, isInvW, # weights matrix
    iters, tolpar, tolparinv, # other params
    ai, pev,
    verbose, retscaled,
    stepweight, emweight
    )

Arguments

Details

This is the Rcpp-coded Direct-Inversion LMM REML algorithm used behind the mmer function.

Value

If all parameters are correctly indicated the program will return a list with the following information:

References

Mrode, R. A. (2014). Linear models for the prediction of animal breeding values. Cabi.

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

See Also

mmes – the core function of the package

Examples

data(DT_cpdata, package="enhancer")
DT <- DT_cpdata

# response matrix
y <- cbind(imputev(DT$Yield), imputev(DT$Firmness))
# fixed effect incidence matrix
X <- model.matrix(~Rowf, data=DT)
# random effect incidence matrix
Z <- Matrix::sparse.model.matrix(~id - 1, data=DT)
colnames(Z) <- gsub("id","",colnames(Z))
# covariance for random effect
GT <- GT_cpdata
A <- A.mat(GT) # additive relationship matrix
A <- A[colnames(Z),colnames(Z)] # make sure of the order
A <- A + diag(1e-4,nrow(A), nrow(A))
# residual effect incidence matrix (dimensions equal nrow(y))
R1 <- Matrix::Diagonal(n=nrow(y)) 
# weights matrix (dimensions equal nrow(y))
W <- diag(nrow(y)) 
# some other parameters
maxIter=3
stepWeight <- rep(0.9, maxIter)
stepWeight[1:2] <- c(0.5, 0.7)
emWeights <- rep(0,maxIter)
# model fit
res <- MNR( Y=y, # multi-trait response
            X=list(X), Gx=list(diag(2)), # fixed effects
            Z=list(Z), K=list(A), # random effects
            R=list(R1), # residual effects
            Ge=list( (diag(2)*.3)+.15 , diag(2)*0.75 ), # inital vc 
            GeI=list(unsm2(2),diag(2)), # vc constraints
            W=W, isInvW=TRUE, # weights for records
            iters=maxIter,
            tolpar=1e-4, tolparinv=1e-6, # tolerance
            ai=FALSE, pev=FALSE, # algorithm specifics
            verbose=TRUE, 
            retscaled=FALSE, 
            stepweight=stepWeight, # second derivatives weights
            emweight=emWeights # em update weights
)
res$sigma
res$Beta
res$U[[1]]

anova form a GLMM fitted with mmes

Description

anova method for class "mmes".

Usage

## S3 method for class 'mmes'
anova(object, object2=NULL, ...)

Arguments

Value

vector of anova

Author(s)

Giovanny Covarrubias

See Also

anova, mmes

atm covariance structure

Description

atm creates a diagonal covariance structure for specific levels of the random effect to be used with the mmes solver.

Usage

  atm(x, levs, thetaC, theta)

Arguments

Value

$res

a list with the provided vector and the variance covariance structure expected.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Examples

x <- as.factor(c(1:5,1:5,1:5));x
atm(x, c("1","2"))
## how to use the theta and thetaC arguments:
# data(DT_example, package="enhancer")
# DT <- DT_example
# theta <- diag(2)*2; theta # initial VCs
# thetaC <- diag(2)*3; thetaC # fixed VCs
# ans1 <- mmes(Yield~Env,
#              random= ~ vsm( atm(Env, levs=c("CA.2013", "CA.2011"),
#                             theta = theta,thetaC = thetaC),ism(Name) ),
#              rcov= ~ units, nIters = 1,
#              data=DT)
# summary(ans1)$varcomp

coef form a GLMM fitted with mmes

Description

coef method for class "mmes".

Usage

## S3 method for class 'mmes'
coef(object, ...)

Arguments

Value

vector of coef

Author(s)

Giovanny Covarrubias

See Also

coef, mmes

Imputing a matrix using correlations

Description

corImputation imputes missing data based on the correlation that exists between row levels.

Usage

  corImputation(wide, Gu=NULL, nearest=10, roundR=FALSE)

Arguments

Value

$res

a list with the imputed matrix and the original matrix.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Examples

####################################
### imputing genotype data example
####################################
# data(DT_cpdata, package="enhancer")
# X <- GT_cpdata
# # add missing data
# v <- sample(1:length(X), 500)
# Xna <- X
# Xna[v]<- NA
# ## impute (can take some time)
# Y <- corImputation(wide=Xna, Gu=NULL, nearest=20, roundR=TRUE) 
# cm <- table(Y$imputed[v],X[v])
# ## calculate accuracy
# sum(diag(cm))/length(v)
####################################
### imputing phenotypic data example
####################################
# data(DT_h2, package="enhancer")
# X <- reshape(DT_h2[,c("Name","Env","y")], direction = "wide", idvar = "Name",
#                 timevar = "Env", v.names = "y", sep= "_")
# rownames(X) <- X$Name
# X <- as.matrix(X[,-1])
# head(X)
# # add missing data
# v <- sample(1:length(X), 50)
# Xna <- X
# Xna[v]<- NA
# ## impute
# Y <- corImputation(wide=Xna, Gu=NULL, nearest=20, roundR=TRUE)
# plot(y=Y$imputed[v],x=X[v], xlab="true",ylab="predicted")
# cor(Y$imputed[v],X[v], use = "complete.obs")

covariance between random effects

Description

covm merges the incidence matrices and covariance matrices of two random effects to fit an unstructured model between 2 different random effects to be fitted with the mmes solver.

Usage

  covm(ran1, ran2, thetaC=NULL, theta=NULL)

Arguments

Details

This implementation aims to fit models where covariance between random variables is expected to exist. For example, indirect genetic effects.

Value

$Z

a incidence matrix Z* = Z Gamma which is the original incidence matrix for the timevar multiplied by the loadings.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Bijma, P. (2014). The quantitative genetics of indirect genetic effects: a selective review of modelling issues. Heredity, 112(1), 61-69.

See Also

The function vsm to know how to use covm in the mmes solver.

Examples

data(DT_ige, package="enhancer")
DT <- DT_ige
covRes <- with(DT, covm( vsm(ism(focal)) , vsm(ism(neighbour)) ) )
str(covRes)
# look at DT_ige help page to see how to fit an actual model

customized covariance structure

Description

csm creates a customized covariance structure for specific levels of the random effect to be used with the mmes solver.

Usage

  csm(x, mm, thetaC, theta)

Arguments

Value

$res

a list with the provided vector and the variance covariance structure expected for the levels of the random effect.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

See Also

The function vsm to know how to use csm in the mmes solver.

Examples

x <- as.factor(c(1:5,1:5,1:5));x
csm(x,matrix(1,5,5))

data frame to matrix

Description

This function takes a matrix that is in data frame format and transforms it into a matrix. Other packages that allows you to obtain an additive relationship matrix from a pedigree is the 'pedigreemm' package.

Usage

  dfToMatrix(x, row="Row",column="Column",
             value="Ainverse", returnInverse=FALSE, 
             bend=1e-6)

Arguments

Value

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Examples

library(Matrix)
m <- matrix(1:9,3,3)
m <- tcrossprod(m)

mdf <- as.data.frame(as.table(m))
mdf

dfToMatrix(mdf, row = "Var1", column = "Var2", 
            value = "Freq",returnInverse=FALSE )

diagonal covariance structure

Description

dsm creates a diagonal covariance structure for the levels of the random effect to be used with the mmes solver.

Usage

  dsm(x, thetaC=NULL, theta=NULL)

Arguments

Value

$res

a list with the provided vector and the variance covariance structure expected for the levels of the random effect.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

See Also

See the function vsm to know how to use dsm in the mmes solver.

Examples

x <- as.factor(c(1:5,1:5,1:5));x
dsm(x)
## how to use the theta and thetaC arguments:
# data(DT_example, package="enhancer")
# DT <- DT_example
# theta <- diag(3)*2; theta # initial VCs
# thetaC <- diag(3)*3; thetaC # fixed VCs
# ans1 <- mmes(Yield~Env,
#              random= ~ vsm( dsm(Env,theta = theta,thetaC = thetaC),ism(Name) ),
#              rcov= ~ units,
#              data=DT)
# summary(ans1)$varcomp

fitted form a LMM fitted with mmes

Description

fitted method for class "mmes".

Usage

## S3 method for class 'mmes'
fitted(object, ...)

Arguments

Value

vector of fitted values of the form y.hat = Xb + Zu including all terms of the model.

Author(s)

Giovanny Covarrubias

See Also

fitted, mmes

Examples

# data(DT_cpdata, package="enhancer")
# DT <- DT_cpdata
# GT <- GT_cpdata
# MP <- MP_cpdata
# #### create the variance-covariance matrix
# A <- A.mat(GT) # additive relationship matrix
# #### look at the data and fit the model
# head(DT)
# mix1 <- mmes(Yield~1,
#               random=~vsm(ism(id),Gu=A)
#                       + Rowf + Colf + spl2Dc(Row,Col),
#               rcov=~units,
#               data=DT)
# 
# ff=fitted(mix1)
# 
# colfunc <- colorRampPalette(c("steelblue4","springgreen","yellow"))
# lattice::wireframe(`u:Row.fitted`~Row*Col, data=ff$dataWithFitted,  
#           aspect=c(61/87,0.4), drape=TRUE,# col.regions = colfunc,
#           light.source=c(10,0,10))
# lattice::levelplot(`u:Row.fitted`~Row*Col, data=ff$dataWithFitted, col.regions = colfunc)

fixed indication matrix

Description

fixm creates a square matrix with 3's in the diagnals and off-diagonals to quickly specify a fixed constraint in the Gtc argument of the vsm function.

Usage

  fixm(x, reps=NULL)

Arguments

Value

$res

a matrix or a list of matrices with the constraints to be provided in the Gtc argument of the vsm function.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Examples

fixm(4)
fixm(4,2)

identity covariance structure

Description

ism creates an identity covariance structure for the levels of the random effect to be used with the mmes solver. Any random effect with a special covariance structure should end with an ism() structure.

Usage

  ism(x, thetaC=NULL, theta=NULL)

Arguments

Value

$res

a list with the provided vector and the variance covariance structure expected for the levels of the random effect.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

See Also

See the function vsm to know how to use ism in the mmes solver.

Examples

x <- as.factor(c(1:5,1:5,1:5));x
ism(x)

# data(DT_example, package="enhancer")
# ans1 <- mmes(Yield~Env,
#              random= ~ vsm( ism( Name ) ),
#              data=DT_example)
# summary(ans1)$varcomp

mixed model equations for r records

Description

The mmer function uses the Direct-Inversion Newton-Raphson or Average Information coded in C++ using the Armadillo library to optimize dense matrix operations common in genomic selection models. These algorithms are intended to be used for problems of the type c > r (more coefficients to estimate than records in the dataset) and/or dense matrices. For problems with sparse data, or problems of the type r > c (more records in the dataset than coefficients to estimate), the MME-based algorithm in the mmes function is faster and we recommend to shift to use that function.

Usage

mmer(fixed, random, rcov, data, weights, W, nIters=20, tolParConvLL = 1e-03, 
     tolParInv = 1e-06, init=NULL, constraints=NULL,method="NR", getPEV=TRUE,
     naMethodX="exclude", naMethodY="exclude",returnParam=FALSE, 
     dateWarning=TRUE,date.warning=TRUE,verbose=TRUE, reshapeOutput=TRUE, stepWeight=NULL,
     emWeight=NULL, contrasts=NULL)

Arguments

Details

The use of this function requires a good understanding of mixed models. Please review the 'sommer.quick.start' vignette and pay attention to details like format of your random and fixed variables (e.g. character and factor variables have different properties when returning BLUEs or BLUPs, please see the 'sommer.changes.and.faqs' vignette).

For tutorials on how to perform different analysis with sommer please look at the vignettes by typing in the terminal:

vignette("v1.sommer.quick.start")

vignette("v2.sommer.changes.and.faqs")

vignette("v3.sommer.qg")

vignette("v4.sommer.gxe")

Citation

Type citation("sommer") to know how to cite the sommer package in your publications.

Special variance structures

vsr(atr(x,levels),y)

can be used to specify heterogeneous variance for the "y" covariate at specific levels of the covariate "x", e.g., random=~vsr(at(Location,c("A","B")),ID) fits a variance component for ID at levels A and B of the covariate Location.

vsr(dsr(x),y)

can be used to specify a diagonal covariance structure for the "y" covariate for all levels of the covariate "x", e.g., random=~vsr(dsr(Location),ID) fits a variance component for ID at all levels of the covariate Location.

vsr(usr(x),y)

can be used to specify an unstructured covariance structure for the "y" covariate for all levels of the covariate "x", e.g., random=~vsr(usr(Location),ID) fits variance and covariance components for ID at all levels of the covariate Location.

vsr(overlay(...,rlist=NULL,prefix=NULL))

can be used to specify overlay of design matrices between consecutive random effects specified, e.g., random=~vsr(overlay(male,female)) overlays (overlaps) the incidence matrices for the male and female random effects to obtain a single variance component for both effects. The 'rlist' argument is a list with each element being a numeric value that multiplies the incidence matrix to be overlayed. See overlay for details.Can be combined with vsr().

vsr(leg(x,n),y)

can be used to fit a random regression model using a numerical variable x that marks the trayectory for the random effect y. The leg function can be combined with the special functions dsr, usr at and csr. For example random=~vsr(leg(x,1),y) or random=~vsr(usr(leg(x,1)),y).

vsr(x,Gtc=fcm(v))

can be used to constrain fixed effects in the multi-response mixed models. This is a vector that specifies if the fixed effect is to be estimated for such trait. For example fixed=cbind(response.i, response.j)~vsr(Rowf, Gtc=fcm(c(1,0))) means that the fixed effect Rowf should only be estimated for the first response and the second should only have the intercept.

gvsr(x,y)

can be used to fit variance and covariance parameters between two or more random effects. For example, indirect genetic effect models.

spl2Da(x.coord, y.coord, at.var, at.levels))

can be used to fit a 2-dimensional spline (e.g., spatial modeling) using coordinates x.coord and y.coord (in numeric class) assuming a single variance component. The 2D spline can be fitted at specific levels using the at.var and at.levels arguments. For example random=~spl2Da(x.coord=Row,y.coord=Range,at.var=FIELD).

spl2Db(x.coord, y.coord, at.var, at.levels))

can be used to fit a 2-dimensional spline (e.g., spatial modeling) using coordinates x.coord and y.coord (in numeric class) assuming multiple variance components. The 2D spline can be fitted at specific levels using the at.var and at.levels arguments. For example random=~spl2Db(x.coord=Row,y.coord=Range,at.var=FIELD).

S3 methods

S3 methods are available for some parameter extraction such as fitted.mmer, residuals.mmer, summary.mmer, randef, coef.mmer, anova.mmer, plot.mmer, and predict.mmer to obtain adjusted means. In addition, the vpredict function (replacement of the pin function) can be used to estimate standard errors for linear combinations of variance components (e.g., ratios like h2).

Additional Functions

Additional functions for genetic analysis have been included such as relationship matrix building (A.mat, D.mat, E.mat, H.mat), build a genotypic hybrid marker matrix (build.HMM), plot of genetic maps (map.plot), and manhattan plots (manhattan). If you need to build a pedigree-based relationship matrix use the getA function from the pedigreemm package.

Bug report and contact

If you have any technical questions or suggestions please post it in https://stackoverflow.com or https://stats.stackexchange.com

If you have any bug report please go to https://github.com/covaruber/sommer or send me an email to address it asap, just make sure you have read the vignettes carefully before sending your question.

Example Datasets

The package has been equiped with several datasets to learn how to use the sommer package:

* DT_halfdiallel, DT_fulldiallel and DT_mohring datasets have examples to fit half and full diallel designs.

* DT_h2 to calculate heritability

* DT_cornhybrids and DT_technow datasets to perform genomic prediction in hybrid single crosses

* DT_wheat dataset to do genomic prediction in single crosses in species displaying only additive effects.

* DT_cpdata dataset to fit genomic prediction models within a biparental population coming from 2 highly heterozygous parents including additive, dominance and epistatic effects.

* DT_polyploid to fit genomic prediction and GWAS analysis in polyploids.

* DT_gryphon data contains an example of an animal model including pedigree information.

* DT_btdata dataset contains an animal (birds) model.

* DT_legendre simulated dataset for random regression model.

* DT_sleepstudy dataset to know how to translate lme4 models to sommer models.

* DT_ige dataset to show how to fit indirect genetic effect models.

Models Enabled

For details about the models enabled and more information about the covariance structures please check the help page of the package (sommer).

Value

If all parameters are correctly indicated the program will return a list with the following information:

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G. Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 2016, 11(6): doi:10.1371/journal.pone.0156744

Covarrubias-Pazaran G. 2018. Software update: Moving the R package sommer to multivariate mixed models for genome-assisted prediction. doi: https://doi.org/10.1101/354639

Bernardo Rex. 2010. Breeding for quantitative traits in plants. Second edition. Stemma Press. 390 pp.

Gilmour et al. 1995. Average Information REML: An efficient algorithm for variance parameter estimation in linear mixed models. Biometrics 51(4):1440-1450.

Kang et al. 2008. Efficient control of population structure in model organism association mapping. Genetics 178:1709-1723.

Lee, D.-J., Durban, M., and Eilers, P.H.C. (2013). Efficient two-dimensional smoothing with P-spline ANOVA mixed models and nested bases. Computational Statistics and Data Analysis, 61, 22 - 37.

Lee et al. 2015. MTG2: An efficient algorithm for multivariate linear mixed model analysis based on genomic information. Cold Spring Harbor. doi: http://dx.doi.org/10.1101/027201.

Maier et al. 2015. Joint analysis of psychiatric disorders increases accuracy of risk prediction for schizophrenia, bipolar disorder, and major depressive disorder. Am J Hum Genet; 96(2):283-294.

Rodriguez-Alvarez, Maria Xose, et al. Correcting for spatial heterogeneity in plant breeding experiments with P-splines. Spatial Statistics 23 (2018): 52-71.

Searle. 1993. Applying the EM algorithm to calculating ML and REML estimates of variance components. Paper invited for the 1993 American Statistical Association Meeting, San Francisco.

Yu et al. 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Genetics 38:203-208.

Tunnicliffe W. 1989. On the use of marginal likelihood in time series model estimation. JRSS 51(1):15-27.

Zhang et al. 2010. Mixed linear model approach adapted for genome-wide association studies. Nat. Genet. 42:355-360.

Examples

####=========================================####
#### For CRAN time limitations most lines in the 
#### examples are silenced with one '#' mark, 
#### remove them and run the examples
####=========================================####

####=========================================####
#### EXAMPLES
#### Different models with sommer
####=========================================####

data(DT_example, package="enhancer")
DT <- DT_example
head(DT)

####=========================================####
#### Univariate homogeneous variance models  ####
####=========================================####

## Compound simmetry (CS) model
ans1 <- mmer(Yield~Env,
             random= ~ Name + Env:Name,
             rcov= ~ units,
             data=DT)
summary(ans1)

####===========================================####
#### Univariate heterogeneous variance models  ####
####===========================================####

## Compound simmetry (CS) + Diagonal (DIAG) model
ans2 <- mmer(Yield~Env,
             random= ~Name + vsr(dsr(Env),Name),
             rcov= ~ vsr(dsr(Env),units),
             data=DT)
summary(ans2)

####===========================================####
####  Univariate unstructured variance models  ####
####===========================================####

ans3 <- mmer(Yield~Env,
             random=~ vsr(usr(Env),Name),
             rcov=~vsr(dsr(Env),units), 
             data=DT)
summary(ans3)



####==========================================####
#### Multivariate homogeneous variance models ####
####==========================================####

## Multivariate Compound simmetry (CS) model
DT$EnvName <- paste(DT$Env,DT$Name)
ans4 <- mmer(cbind(Yield, Weight) ~ Env,
              random= ~ vsr(Name, Gtc = unsm(2)) + vsr(EnvName,Gtc = unsm(2)),
              rcov= ~ vsr(units, Gtc = unsm(2)),
              data=DT)
summary(ans4)

####=============================================####
#### Multivariate heterogeneous variance models  ####
####=============================================####

## Multivariate Compound simmetry (CS) + Diagonal (DIAG) model
ans5 <- mmer(cbind(Yield, Weight) ~ Env,
              random= ~ vsr(Name, Gtc = unsm(2)) + vsr(dsr(Env),Name, Gtc = unsm(2)),
              rcov= ~ vsr(dsr(Env),units, Gtc = unsm(2)),
              data=DT)
summary(ans5)

####===========================================####
#### Multivariate unstructured variance models ####
####===========================================####

ans6 <- mmer(cbind(Yield, Weight) ~ Env,
              random= ~ vsr(usr(Env),Name, Gtc = unsm(2)),
              rcov= ~ vsr(dsr(Env),units, Gtc = unsm(2)),
              data=DT)
summary(ans6)

####=========================================####
####=========================================####
#### EXAMPLE SET 2
#### 2 variance components
#### one random effect with variance covariance structure
####=========================================####
####=========================================####

data("DT_cpdata", package="enhancer")
DT <- DT_cpdata
GT <- GT_cpdata
MP <- MP_cpdata
head(DT)
GT[1:4,1:4]
#### create the variance-covariance matrix
A <- A.mat(GT)
#### look at the data and fit the model
mix1 <- mmer(Yield~1,
             random=~vsr(id, Gu=A) + Rowf,
             rcov=~units,
             data=DT)
summary(mix1)$varcomp

#### multi trait example
mix2 <- mmer(cbind(Yield,color)~1,
              random = ~ vsr(id, Gu=A, Gtc = unsm(2)) + # unstructured at trait level
                            vsr(Rowf, Gtc=diag(2)) + # diagonal structure at trait level
                                vsr(Colf, Gtc=diag(2)), # diagonal structure at trait level
              rcov = ~ vsr(units, Gtc = unsm(2)), # unstructured at trait level
              data=DT)
summary(mix2)

mixed model equations solver

Description

The mmes function uses either the direct inversion or the Henderson mixed model equations algorithms coded in C++ using the Armadillo library to optimize matrix operations. For problems of the type c > r (more coefficients to estimate than records available), the direct inversion algorithm is faster (using the argument henderson=FALSE; default). For more records than coefficients set henderson=TRUE and make sure that you provide the relationship matrix as an inverse (see vsm() function for details).

Usage

mmes(fixed, random, rcov, data, W, nIters=50, tolParConvLL = 1e-04,
     tolParConvNorm = 1e-04, tolParInv = 1e-06, naMethodX="exclude",
     naMethodY="exclude", returnParam=FALSE, dateWarning=TRUE,
     verbose=TRUE,addScaleParam=NULL, stepWeight=NULL, emWeight=NULL,
     contrasts=NULL, getPEV=TRUE, henderson=FALSE)

Arguments

Details

The use of this function requires a good understanding of mixed models. Please review the 'sommer.quick.start' vignette and pay attention to details like format of your random and fixed variables (e.g. character and factor variables have different properties when returning BLUEs or BLUPs).

For tutorials on how to perform different analysis with sommer please look at the vignettes by typing in the terminal:

vignette("v1.sommer.quick.start")

vignette("v2.sommer.changes.and.faqs")

vignette("v3.sommer.qg")

vignette("v4.sommer.gxe")

Citation

Type citation("sommer") to know how to cite the sommer package in your publications.

Special variance structures

vsm(atm(x,levels),ism(y))

can be used to specify heterogeneous variance for the "y" covariate at specific levels of the covariate "x", e.g., random=~vsm(at(Location,c("A","B")),ism(ID)) fits a variance component for ID at levels A and B of the covariate Location.

vsm(dsm(x),ism(y))

can be used to specify a diagonal covariance structure for the "y" covariate for all levels of the covariate "x", e.g., random=~vsm(dsm(Location),ism(ID)) fits a variance component for ID at all levels of the covariate Location.

vsm(usm(x),ism(y))

can be used to specify an unstructured covariance structure for the "y" covariate for all levels of the covariate "x", e.g., random=~vsm(usm(Location),ism(ID)) fits variance and covariance components for ID at all levels of the covariate Location.

vsm(usm(rrm(x,y,z,nPC)),ism(y))

can be used to specify an unstructured covariance structure for the "y" effect for all levels of the covariate "x", and a response variable "z", e.g., random=~vsm(rrm(Location,ID,response, nPC=2),ism(ID)) fits a reduced-rank factor analytic covariance for ID at 2 principal components of the covariate Location.

vsm(ism(overlay(...,rlist=NULL,prefix=NULL)))

can be used to specify overlay of design matrices between consecutive random effects specified, e.g., random=~vsm(ism(overlay(male,female))) overlays (overlaps) the incidence matrices for the male and female random effects to obtain a single variance component for both effects. The 'rlist' argument is a list with each element being a numeric value that multiplies the incidence matrix to be overlayed. See overlay for details.Can be combined with vsm().

vsm(ism(redmm(x,M,nPC)))

can be used to create a reduced model matrix of an effect (x) assumed to be a linear function of some feature matrix (M), e.g., random=~vsm(ism(redmm(x,M))) creates an incidence matrix from a very large set of features (M) that belong to the levels of x to create a reduced model matrix. See redmm for details.Can be combined with vsm().

vsm(leg(x,n),ism(y))

can be used to fit a random regression model using a numerical variable x that marks the trayectory for the random effect y. The leg function can be combined with the special functions dsm, usm at and csm. For example random=~vsm(leg(x,1),ism(y)) or random=~vsm(usm(leg(x,1)),ism(y)).

spl2Dc(x.coord, y.coord, at.var, at.levels))

can be used to fit a 2-dimensional spline (e.g., spatial modeling) using coordinates x.coord and y.coord (in numeric class) assuming multiple variance components. The 2D spline can be fitted at specific levels using the at.var and at.levels arguments. For example random=~spl2Dc(x.coord=Row,y.coord=Range,at.var=FIELD).

Covariance between random effects

covm( vsm(ism(ran1)), vsm(ism(ran2)) )

can be used to specify covariance between two different random effects, e.g., random=~covm( vsm(ism(x1)), vsm(ism(x2)) ) where two random effects in their own vsm() structure are encapsulated. Only applies for simple random effects.

S3 methods

S3 methods are available for some parameter extraction such as fitted.mmes, residuals.mmes, summary.mmes, randef, coef.mmes, anova.mmes, plot.mmes, and predict.mmes to obtain adjusted means. In addition, the vpredict function (replacement of the pin function) can be used to estimate standard errors for linear combinations of variance components (e.g., ratios like h2). The r2 function calculates reliability.

Additional Functions

Additional functions for genetic analysis have been included such as relationship matrix building (A.mat, D.mat, E.mat, H.mat), build a genotypic hybrid marker matrix (build.HMM), plot of genetic maps (map.plot), and manhattan plots (manhattan). If you need to build a pedigree-based relationship matrix use the getA function from the pedigreemm package.

Bug report and contact

If you have any technical questions or suggestions please post it in https://stackoverflow.com or https://stats.stackexchange.com

If you have any bug report please go to https://github.com/covaruber/sommer or send me an email to address it asap, just make sure you have read the vignettes carefully before sending your question.

Example Datasets

The package has been equiped with several datasets to learn how to use the sommer package:

* DT_halfdiallel, DT_fulldiallel and DT_mohring datasets have examples to fit half and full diallel designs.

* DT_h2 to calculate heritability

* DT_cornhybrids and DT_technow datasets to perform genomic prediction in hybrid single crosses

* DT_wheat dataset to do genomic prediction in single crosses in species displaying only additive effects.

* DT_cpdata dataset to fit genomic prediction models within a biparental population coming from 2 highly heterozygous parents including additive, dominance and epistatic effects.

* DT_polyploid to fit genomic prediction and GWAS analysis in polyploids.

* DT_gryphon data contains an example of an animal model including pedigree information.

* DT_btdata dataset contains an animal (birds) model.

* DT_legendre simulated dataset for random regression model.

* DT_sleepstudy dataset to know how to translate lme4 models to sommer models.

* DT_ige dataset to show how to fit indirect genetic effect models.

Models Enabled

For details about the models enabled and more information about the covariance structures please check the help page of the package (sommer).

Value

If all parameters are correctly indicated the program will return a list with the following information:

Author(s)

Coded by Giovanny Covarrubias-Pazaran with contributions of Christelle Fernandez Camacho to the henderson algorithm.

References

Covarrubias-Pazaran G. Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 2016, 11(6): doi:10.1371/journal.pone.0156744

Jensen, J., Mantysaari, E. A., Madsen, P., and Thompson, R. (1997). Residual maximum likelihood estimation of (co) variance components in multivariate mixed linear models using average information. Journal of the Indian Society of Agricultural Statistics, 49, 215-236.

Sanderson, C., & Curtin, R. (2025). Armadillo: An Efficient Framework for Numerical Linear Algebra. arXiv preprint arXiv:2502.03000.

Gilmour et al. 1995. Average Information REML: An efficient algorithm for variance parameter estimation in linear mixed models. Biometrics 51(4):1440-1450.

Examples

####=========================================####
#### For CRAN time limitations most lines in the
#### examples are silenced with one '#' mark,
#### remove them and run the examples
####=========================================####

data(DT_example, package="enhancer")
DT <- DT_example
head(DT)

####=========================================####
#### Univariate homogeneous variance models  ####
####=========================================####

## Compound simmetry (CS) model
ans1 <- mmes(Yield~Env,
             random= ~ Name + Env:Name,
             rcov= ~ units,
             data=DT)
summary(ans1)



####===========================================####
#### Univariate heterogeneous variance models  ####
####===========================================####
DT=DT[with(DT, order(Env)), ]
## Compound simmetry (CS) + Diagonal (DIAG) model
ans2 <- mmes(Yield~Env,
             random= ~Name + vsm(dsm(Env),ism(Name)),
             rcov= ~ vsm(dsm(Env),ism(units)),
             data=DT)
summary(ans2)

####===========================================####
####  Univariate unstructured variance models  ####
####===========================================####

ans3 <- mmes(Yield~Env,
             random=~ vsm(usm(Env),ism(Name)),
             rcov=~vsm(dsm(Env),ism(units)),
             data=DT)
summary(ans3)

plot form a LMM plot with mmes

Description

plot method for class "mmes".

Usage

## S3 method for class 'mmes'
plot(x,stnd=TRUE, ...)

Arguments

Value

vector of plot

Author(s)

Giovanny Covarrubias covarrubiasp@wisc.edu

See Also

plot, mmes

Examples

data(DT_yatesoats, package="enhancer")
DT <- DT_yatesoats
head(DT)
m3 <- mmes(fixed=Y ~ V + N + V:N,
           random = ~ B + B:MP,
           rcov=~units,
           data = DT)
plot(m3)

plot the change of VC across iterations

Description

plot for monitoring.

Usage

pmonitor(object, ...)

Arguments

Value

vector of plot

Author(s)

Giovanny Covarrubias

See Also

plot, mmes

Examples

data(DT_yatesoats, package="enhancer")
DT <- DT_yatesoats
head(DT)
m3 <- mmes(fixed=Y ~ V + N + V:N,
           random = ~ B + B:MP,
           rcov=~units,
           data = DT)
pmonitor(m3)

Predict form of a LMM fitted with mmes

Description

predict method for class "mmes".

Usage

## S3 method for class 'mmes'
predict(object, Dtable=NULL, D, ...)

Arguments

Details

This function allows to produce predictions specifying those variables that define the margins of the hypertable to be predicted (argument D). Predictions are obtained for each combination of values of the specified variables that is present in the data set used to fit the model. See vignettes for more details.

For predicted values the pertinent design matrices X and Z together with BLUEs (b) and BLUPs (u) are multiplied and added together.

predicted.value equal Xb + Zu.1 + ... + Zu.n

For computing standard errors for predictions the parts of the coefficient matrix:

C11 equal (X.t() V.inv() X).inv()

C12 equal 0 - [(X.t() V.inv() X).inv() X.t() V.inv() G Z]

C22 equal PEV equal G - [Z.t() G[V.inv() - (V.inv() X X.t() V.inv() X V.inv() X)]G Z.t()]

In practive C equals ( W.t() V.inv() W ).inv()

when both fixed and random effects are present in the inclusion set. If only fixed and random effects are included, only the respective terms from the SE for fixed or random effects are calculated.

Value

Author(s)

Giovanny Covarrubias-Pazaran

References

Welham, S., Cullis, B., Gogel, B., Gilmour, A., and Thompson, R. (2004). Prediction in linear mixed models. Australian and New Zealand Journal of Statistics, 46, 325 - 347.

See Also

predict, mmes

Examples

data(DT_yatesoats, package="enhancer")
DT <- DT_yatesoats
m3 <- mmes(fixed=Y ~ V + N + V:N ,
           random = ~ B + B:MP,
           rcov=~units,
           data = DT)

#############################
## predict means for nitrogen
#############################
Dt <- m3$Dtable; Dt
# first fixed effect just average
Dt[1,"average"] = TRUE
# second fixed effect include
Dt[2,"include"] = TRUE
# third fixed effect include and average
Dt[3,"include"] = TRUE
Dt[3,"average"] = TRUE
Dt

pp=predict(object=m3, Dtable=Dt, D="N")
pp$pvals

#############################
## predict means for variety
#############################

Dt <- m3$Dtable; Dt
# first fixed effect include
Dt[1,"include"] = TRUE
# second fixed effect just average
Dt[2,"average"] = TRUE
# third fixed effect include and average
Dt[3,"include"] = TRUE
Dt[3,"average"] = TRUE
Dt

pp=predict(object=m3, Dtable=Dt, D="V")
pp$pvals

#############################
## predict means for nitrogen:variety
#############################
# prediction matrix D based on (equivalent to classify in asreml)
Dt <- m3$Dtable; Dt
# first fixed effect include and average
Dt[1,"include"] = TRUE
Dt[1,"average"] = TRUE
# second fixed effect include and average
Dt[2,"include"] = TRUE
Dt[2,"average"] = TRUE
# third fixed effect include and average
Dt[3,"include"] = TRUE
Dt[3,"average"] = TRUE
Dt

pp=predict(object=m3, Dtable=Dt, D="N:V")
pp$pvals

Reliability

Description

Calculates the reliability of BLUPs in a sommer model.

Usage

r2(object, object2=NULL)

Arguments

Details

The reliability method calculated is the classical animal model: R2=(G-PEV)/G

Value

result

a list with as many elements as random effects fitted containing reliabilities for individual BLUPs.

References

Mrode, R. A. (2014). Linear models for the prediction of animal breeding values. Cabi.

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

See Also

mmes – the core function of the package

Examples

####=========================================####
#### Example population
####=========================================####
data(DT_example, package="enhancer")
DT <- DT_example
head(DT)
ans1 <- mmes(Yield~Env, 
             random= ~ Name + Env:Name,
             rcov= ~ units,
             data=DT)
rel=r2(ans1)

extracting random effects

Description

This function is extracts the random effects from a mixed model fitted by mmer.

Usage

randef(object)

Arguments

Value

$randef

a list structure with the random effects or BLUPs.

Examples

# randef(model)

Residuals form a GLMM fitted with mmes

Description

residuals method for class "mmes".

Usage

## S3 method for class 'mmes'
residuals(object, ...)

Arguments

Value

vector of residuals of the form e = y - Xb - Zu, the so called conditional residuals.

Author(s)

Giovanny Covarrubias

See Also

residuals, mmes

Solving Mixed Model Equations in R

Description

Sommer is a structural multivariate-univariate linear mixed model solver for multiple random effects allowing the specification and/or estimation of variance covariance structures. REML estimates can be obtained using two major methods

Direct-Inversion (Newton-Raphson and Average Information)

Henderson's mixed model equations (Average Information)

The algorithms are coded in C++ using the Armadillo library to optimize dense matrix operations common in genomic models. Sommer was designed to include complex covariance structures, e.g., unstructured, reduced-rank, diagonal. And also to model relationships between levels of a random effect, e.g., additive, dominance and epistatic relationship structures.

The direct inversion algorithm available in the mmes function (argument henderson=FALSE) can deal well with small and medium-size data sets (< 10,000 observations/records for average computers given the computational burden carried by the direct-inversion algorithms) since it works in the c > r problem and inverts an r x r matrix (being r the number of records and c the number of coefficients). On the other hand, the Henderson algorithm in the mmes function (argument henderson=TRUE) can deal with greater number of records (r>250K) as long as the number of coefficients to estimate is < 10,000 coefficients (c) since it works in the r > c problem and inverts a c x c matrix (being c the number of coefficients). The predict.mmes function can be used to obtain adjusted means. This package returns variance-covariance components, BLUPs, BLUEs, residuals, fitted values, variances-covariances for fixed and random effects, etc.

Functions for genetic analysis

The package provides kernels to estimate additive (A.mat), dominance (D.mat), epistatic (E.mat), single-step (H.mat) relationship matrices for diploid and polyploid organisms. It also provides flexibility to fit other genetic models such as full and half diallel models and random regression models.

A good converter from letter code to numeric format is implemented in the function atcg1234, which supports higher ploidy levels than diploid. Additional functions for genetic analysis have been included such as build a genotypic hybrid marker matrix (build.HMM), plot of genetic maps (map.plot), creation of manhattan plots (manhattan). If you need to use pedigree you need to convert your pedigree into a relationship matrix (use the 'getA' function from the pedigreemm package).

Functions for statistical analysis and S3 methods

The vpredict function can be used to estimate standard errors for linear combinations of variance components (e.g. ratios like h2). The r2 function calculates reliability. S3 methods are available for some parameter extraction such as:

+ predict.mmes

+ fitted.mmes

+ residuals.mmes

+ summary.mmes

+ coef.mmes

+ anova.mmes

+ plot.mmes

Functions for trial analysis

Recently, spatial modeling has been added added to sommer using the two-dimensional spline (spl2Dc).

Keeping sommer updated

The sommer package is updated on CRAN every 4-months due to CRAN policies but you can find the latest source at https://github.com/covaruber/sommer. This can be easily installed typing the following in the R console:

library(devtools)

install_github("covaruber/sommer")

This is recommended if you reported a bug, was fixed and was immediately pushed to GitHub but not in CRAN until the next update.

Tutorials

For tutorials on how to perform different analysis with sommer please look at the vignettes by typing in the terminal:

vignette("sommer.qg")

vignette("sommer.gxe")

vignette("sommer.vs.lme4")

vignette("sommer.spatial")

Getting started

The package has been equiped with several datasets to learn how to use the sommer package (and almost to learn all sort of quantitative genetic analysis):

* DT_halfdiallel, DT_fulldiallel and DT_mohring datasets have examples to fit half and full diallel designs.

* DT_h2 to calculate heritability

* DT_cornhybrids and DT_technow datasets to perform genomic prediction in hybrid single crosses

* DT_wheat dataset to do genomic prediction in single crosses in species displaying only additive effects.

* DT_cpdata dataset to fit genomic prediction models within a biparental population coming from 2 highly heterozygous parents including additive, dominance and epistatic effects.

* DT_polyploid to fit genomic prediction and GWAS analysis in polyploids.

* DT_gryphon data contains an example of an animal model including pedigree information.

* DT_btdata dataset contains an animal (birds) model.

* DT_legendre simulated dataset for random regression model.

* DT_sleepstudy dataset to know how to translate lme4 models to sommer models.

Differences of sommer >= 4.4.1 with previous versions

Since version 4.4.1, I have unified the use of the two different solving algorithms into the mmes function by just using the new argument henderson which by default is set to FALSE. Other than that the rest is the same with the addition that now the identity terms needs to be encapsulated in the ism function. In addition, now the multi-trait models need to be fitted in the long format. This are few but major changes to the way sommer models are fitted.

Differences of sommer >= 4.1.7 with previous versions

Since version 4.1.7 I have introduced the mmes-based average information function 'mmec' which is much faster when dealing with the r > c problem (more records than coefficients to estimate). This introduces its own covariance structure functons such as vsc(), usc(), dsc(), atc(), csc(). Please give it a try, although is in early phase of development.

Differences of sommer >= 3.7.0 with previous versions

Since version 3.7 I have completly redefined the specification of the variance-covariance structures to provide more flexibility to the user. This has particularly helped the residual covariance structures and the easier combination of custom random effects and overlay models. I think that although this will bring some uncomfortable situations at the beggining, in the long term this will help users to fit better models. In esence, I have abandoned the asreml formulation (not the structures available) given it's limitations to combine some of the sommer structures but all covariance structures can now be fitted using the 'vsm' functions.

Differences of sommer >= 3.0.0 with previous versions

Since version 3.0 I have decided to focus in developing the multivariate solver and for doing this I have decided to remove the M argument (for GWAS analysis) from the mmes function and move it to it's own function GWAS.

Before the mmes solver had implemented the usm(trait), diag(trait), at(trait) asreml formulation for multivariate models that allow to specify the structure of the trait in multivariate models. Therefore the MVM argument was no longer needed. After version 3.7 now the multi-trait structures can be specified in the Gt and Gtc arguments of the vsm function.

The Average Information algorithm had been removed in the past from the package because of its instability to deal with very complex models without good initial values. Now after 3.7 I have brought it back after I noticed that starting with NR the first three iterations gives enough flexibility to the AI algorithm.

Keep in mind that sommer uses direct inversion (DI) algorithm which can be very slow for datasets with many observations (big 'n'). The package is focused in problems of the type p > n (more random effect(s) levels than observations) and models with dense covariance structures. For example, for experiment with dense covariance structures with low-replication (i.e. 2000 records from 1000 individuals replicated twice with a covariance structure of 1000x1000) sommer will be faster than MME-based software. Also for genomic problems with large number of random effect levels, i.e. 300 individuals (n) with 100,000 genetic markers (p). On the other hand, for highly replicated trials with small covariance structures or n > p (i.e. 2000 records from 200 individuals replicated 10 times with covariance structure of 200x200) asreml or other MME-based algorithms will be much faster and I recommend you to use that software.

Models Enabled

The core of the package are the mmes (formula-based) function which solve the mixed model equations. The functions are an interface to call the 'NR' Direct-Inversion Newton-Raphson, 'AI' Direct-Inversion Average Information or the mmes-based Average Information (Tunnicliffe 1989; Gilmour et al. 1995; Lee et al. 2016). Since version 2.0 sommer can handle multivariate models. Following Maier et al. (2015), the multivariate (and by extension the univariate) mixed model implemented has the form:

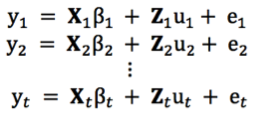
where y_i is a vector of trait phenotypes, \beta_i is a vector of fixed effects, u_i is a vector of random effects for individuals and e_i are residuals for trait i (i = 1,..., t). The random effects (u_1 ... u_i and e_i) are assumed to be normally distributed with mean zero. X and Z are incidence matrices for fixed and random effects respectively. The distribution of the multivariate response and the phenotypic variance covariance (V) are:

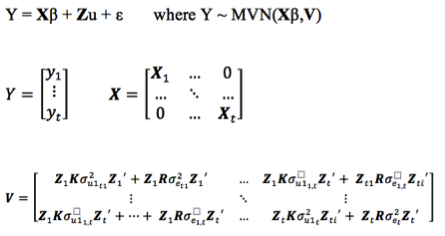
where K is the relationship or covariance matrix for the kth random effect (u=1,...,k), and R=I is an identity matrix for the residual term. The terms \sigma^2_{g_{i}} and \sigma^2_{\epsilon_{i}} denote the genetic (or any of the kth random terms) and residual variance of trait i, respectively and \sigma_{g_{_{ij}}} and \sigma_{\epsilon_{_{ij}}} the genetic (or any of the kth random terms) and residual covariance between traits i and j (i=1,...,t, and j=1,...,t). The algorithm implemented optimizes the log likelihood:

where || is the determinant of a matrix. And the REML estimates are updated using a Newton optimization algorithm of the form:

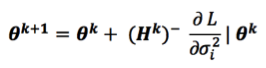
Where, theta is the vector of variance components for random effects and covariance components among traits, H^-1 is the inverse of the Hessian matrix of second derivatives for the kth cycle, dL/dsigma^2_i is the vector of first derivatives of the likelihood with respect to the variance-covariance components. The Eigen decomposition of the relationship matrix proposed by Lee and Van Der Werf (2016) was included in the Newton-Raphson algorithm to improve time efficiency. Additionally, the popular vpredict function to estimate standard errors for linear combinations of variance components (i.e. heritabilities and genetic correlations) was added to the package as well.

Bug report and contact

If you have any questions or suggestions please post it in https://stackoverflow.com or https://stats.stackexchange.com

I'll be glad to help or answer any question. I have spent a valuable amount of time developing this package. Please cite this package in your publication. Type 'citation("sommer")' to know how to cite it.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G. 2016. Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Covarrubias-Pazaran G. 2018. Software update: Moving the R package sommer to multivariate mixed models for genome-assisted prediction. doi: https://doi.org/10.1101/354639

Sanderson, C., & Curtin, R. (2025). Armadillo: An Efficient Framework for Numerical Linear Algebra. arXiv preprint arXiv:2502.03000.

Bernardo Rex. 2010. Breeding for quantitative traits in plants. Second edition. Stemma Press. 390 pp.

Gilmour et al. 1995. Average Information REML: An efficient algorithm for variance parameter estimation in linear mixed models. Biometrics 51(4):1440-1450.

Henderson C.R. 1975. Best Linear Unbiased Estimation and Prediction under a Selection Model. Biometrics vol. 31(2):423-447.

Kang et al. 2008. Efficient control of population structure in model organism association mapping. Genetics 178:1709-1723.

Lee et al. 2015. MTG2: An efficient algorithm for multivariate linear mixed model analysis based on genomic information. Cold Spring Harbor. doi: http://dx.doi.org/10.1101/027201.

Maier et al. 2015. Joint analysis of psychiatric disorders increases accuracy of risk prediction for schizophrenia, bipolar disorder, and major depressive disorder. Am J Hum Genet; 96(2):283-294.

Searle. 1993. Applying the EM algorithm to calculating ML and REML estimates of variance components. Paper invited for the 1993 American Statistical Association Meeting, San Francisco.

Yu et al. 2006. A unified mixed-model method for association mapping that accounts for multiple levels of relatedness. Genetics 38:203-208.

Tunnicliffe W. 1989. On the use of marginal likelihood in time series model estimation. JRSS 51(1):15-27.

Examples

####=========================================####
#### For CRAN time limitations most lines in the 
#### examples are silenced with one '#' mark, 
#### remove them and run the examples
####=========================================####

####=========================================####
#### EXAMPLES
#### Different models with sommer
####=========================================####

data(DT_example, package="enhancer")





DT <- DT_example
DT=DT[with(DT, order(Env)), ]
head(DT)

####=========================================####
#### Univariate homogeneous variance models  ####
####=========================================####

## Compound simmetry (CS) model
ans1 <- mmes(Yield~Env,
             random= ~ Name + Env:Name,
             rcov= ~ units,
             data=DT)
summary(ans1)

####===========================================####
#### Univariate heterogeneous variance models  ####
####===========================================####
## Compound simmetry (CS) + Diagonal (DIAG) model
ans3 <- mmes(Yield~Env,
             random= ~Name + vsm(dsm(Env),ism(Name)),
             rcov= ~ vsm(dsm(Env),ism(units)),
             data=DT)
summary(ans3)

Two-dimensional penalised tensor-product of marginal B-Spline basis.

Description

Auxiliary function used for modelling the spatial or environmental effect as a two-dimensional penalised tensor-product (isotropic approach) based on Lee et al. (2013) and Rodriguez-Alvarez et al. (2018). This is a modified wrapper of some portions of the SpATS package to build a single incidence matrix containing all the columns from tensor products of the x and y coordinates and it fits such matrix as a single random effect. Then the heterogeneous covariances structure capabilities of sommer can be used to enhance the model fit. You may be interested in reading and citing not only sommec but also Wageningen publications if using this 2D spline methodology.

Usage

spl2Dc(x.coord,y.coord,at.var=NULL,at.levels=NULL, type="PSANOVA", 
      nsegments = c(10,10), penaltyord = c(2,2), degree = c(3,3), 
      nestorder = c(1,1), thetaC=NULL, theta=NULL, sp=FALSE)

Arguments

Details

The following documentation is taken from the SpATS package. Please refer to this package and associated publications if you are interested in going deeper on this technique:

Within the P-spline framework, anisotropic low-rank tensor-product smoothers have become the general approach for modelling multidimensional surfaces (Eilers and Marx 2003; Wood 2006). In the original SpATS package, was proposed to model the spatial or environmental effect by means of the tensor-product of B-splines basis functions. In other words, was proposed to model the spatial trend as a smooth bivariate surface jointly defined over the the spatial coordinates. Accordingly, the current function has been designed to allow the user to specify the spatial coordinates that the spatial trend is a function of. There is no restriction about how the spatial coordinates shall be specified: these can be the longitude and latitude of the position of the plot on the field or the column and row numbers. The only restriction is that the variables defining the spatial coordinates should be numeric (in contrast to factors).

As far as estimation is concerned, we have used in this package the equivalence between P-splines and linear mixed models (Currie and Durban, 2002). Under this approach, the smoothing parameters are expressed as the ratio between variance components. Moreover, the smooth components are decomposed in two parts: one which is not penalised (and treated as fixed) and one with is penalised (and treated as random). For the two-dimensional case, the mixed model representation leads also to a very interesting decomposition of the penalised part of the bivariate surface in three different components (Lee and Durban, 2011): (a) a component that contains the smooth main effect (smooth trend) along one of the covariates that the surface is a function of (as, e.g, the x-spatial coordinate or column position of the plot in the field), (b) a component that contains the smooth main effect (smooth trend) along the other covariate (i.e., the y-spatial coordinate or row position); and (c) a smooth interaction component (sum of the linear-by-smooth interaction components and the smooth-by-smooth interaction component).

The original implementation of SpATS assumes two different smoothing parameters, i.e., one for each covariate in the smooth component. Accordingly, the same smoothing parameters are used for both, the main effects and the smooth interaction. However, this approach can be extended to deal with the ANOVA-type decomposition presented in Lee and Durban (2011). In their approach, four different smoothing parameters are considered for the smooth surface, that are in concordance with the aforementioned decomposition: (a) two smoothing parameter, one for each of the main effects; and (b) two smoothing parameter for the smooth interaction component.

It should be noted that, the computational burden associated with the estimation of the two-dimensional tensor-product smoother might be prohibitive if the dimension of the marginal bases is large. In these cases, Lee et al. (2013) propose to reduce the computational cost by using nested bases. The idea is to reduce the dimension of the marginal bases (and therefore the associated number of parameters to be estimated), but only for the smooth-by-smooth interaction component. As pointed out by the authors, this simplification can be justified by the fact that the main effects would in fact explain most of the structure (or spatial trend) presented in the data, and so a less rich representation of the smooth-by-smooth interaction component could be needed. In order to ensure that the reduced bivariate surface is in fact nested to the model including only the main effects, Lee et al. (2013) show that the number of segments used for the nested basis should be a divisor of the number of segments used in the original basis (nsegments argument). In the present function, the divisor of the number of segments is specified through the argument nestorder. For a more detailed review on this topic, see Lee (2010) and Lee et al. (2013). The "PSANOVA" approach represents an alternative method. In this case, the smooth bivariate surface (or spatial trend) is decomposed in five different components each of them depending on a single smoothing parameter (see Lee et al., 2013).

—————–

As mentioned at the beginning, the piece of documentation stated above was taken completely from the SpATS package in order to provide a deeper explanation. In practice, sommec uses some pieces of code from SpATS to build the design matrix containing all the columns from tensor products of the x and y coordinates and it fits such matrix as a single random effect. As a result the same variance component is assumed for the linear, linear by linear, linear by spline, and spline by spline interactions. This results in a less flexible approach than the one proposed by Rodriguez-Alvarez et al. (2018) but still makes a pretty good job to model the spatial variation. Use under your own risk.

References

Rodriguez-Alvarez, M.X, Boer, M.P., van Eeuwijk, F.A., and Eilers, P.H.C. (2018). SpATS: Spatial Analysis of Field Trials with Splines. R package version 1.0-9. https://CRAN.R-project.org/package=SpATS.

Rodriguez-Alvarez, M.X., et al. (2015) Fast smoothng parameter separaton n multdmensonal generalzed P-splnes: the SAP algorthm. Statistics and Computing 25.5: 941-957.

Lee, D.-J., Durban, M., and Eilers, P.H.C. (2013). Efficient two-dimensional smoothing with P-spline ANOVA mixed models and nested bases. Computational Statistics and Data Analysis, 61, 22 - 37.

Gilmour, A.R., Cullis, B.R., and Verbyla, A.P. (1997). Accounting for Natural and Extraneous Variation in the Analysis of Field Experiments. Journal of Agricultural, Biological, and Environmental Statistics, 2, 269 - 293.

See Also

mmes

Examples

## ============================ ##
## example to use spl2Dc() 
## ============================ ## 
data(DT_cpdata, package="enhancer")
# DT <- DT_cpdata
# GT <- GT_cpdata
# MP <- MP_cpdata
# A <- A.mat(GT)
## ============================ ##
## mimic 2 fields
## ============================ ## 
# aa <- DT; bb <- DT
# aa$FIELD <- "A";bb$FIELD <- "B"
# set.seed(1234)
# aa$Yield <- aa$Yield + rnorm(length(aa$Yield),0,4)
# DT2 <- rbind(aa,bb)
# head(DT2)
# mix <- mmes(Yield~1, henderson = F,
#             random=~
#               vsm(dsm(FIELD),ism(Rowf)) +
#               vsm(dsm(FIELD),ism(Colf)) +
#                 spl2Dc(Row,Col,at.var=FIELD),
#             rcov=~vsm(dsm(FIELD),ism(units)),
#             data=DT2)
# 
# # extract spatial effects
# blup <- mix$uList$`spl2Dc(Row, Col, at.var = FIELD`
# head(blup) # 2 fields
# # recreate the incidence matrices
# xx=with(DT2, spl2Dc(Row,Col,at.var=FIELD))
# # get fitted values Zu for spatial effects and add them to the dataset
# field1 <- xx$Z$`A:all` %*% blup[,1]
# field2 <- xx$Z$`B:all` %*% blup[,2]
# DT2$spat <- field1+field2
# # plots the spatial effects
# lattice::levelplot(spat~Row*Col|FIELD, data=DT2)

Get Tensor Product Spline Mixed Model Incidence Matrices

Description

spl2Dmats gets Tensor-Product P-Spline Mixed Model Incidence Matrices for use with sommer and its main function mmes. We thank Sue Welham for making the TPSbits package available to the community. If you're using this function for your research please cite her TPSbits package :) this is mostly a wrapper of her tpsmmb function to enable the use in sommer.

Usage

spl2Dmats(
  x.coord.name,
  y.coord.name,
  data,
  at.name,
  at.levels, 
  nsegments=NULL,
  minbound=NULL,
  maxbound=NULL,
  degree = c(3, 3),
  penaltyord = c(2,2), 
  nestorder = c(1,1),
  method = "Lee"
)

Arguments

Value

List of length 7 elements:

1. data = the input data frame augmented with structures required to fit tensor product splines in asreml-R. This data frame can be used to fit the TPS model.

   Added columns:

   • TP.col, TP.row = column and row coordinates

   • TP.CxR = combined index for use with smooth x smooth term

   • TP.C.n for n=1:(diff.c) = X parts of column spline for use in random model (where diff.c is the order of column differencing)

   • TP.R.n for n=1:(diff.r) = X parts of row spline for use in random model (where diff.r is the order of row differencing)

   • TP.CR.n for n=1:((diff.c*diff.r)) = interaction between the two X parts for use in fixed model. The first variate is a constant term which should be omitted from the model when the constant (1) is present. If all elements are included in the model then the constant term should be omitted, eg. y ~ -1 + TP.CR.1 + TP.CR.2 + TP.CR.3 + TP.CR.4 + other terms...

   • when asreml="grp" or "sepgrp", the spline basis functions are also added into the data frame. Column numbers for each term are given in the grp list structure.

2. fR = Xr1:Zc

3. fC = Xr2:Zc

4. fR.C = Zr:Xc1

5. R.fC = Zr:Xc2

6. fR.fC = Zc:Zr

7. all = Xr1:Zc | Xr2:Zc | Zr:Xc1 | Zr:Xc2 | Zc:Zr

Examples

data("DT_cpdata", package="enhancer")
DT <- DT_cpdata
GT <- GT_cpdata
MP <- MP_cpdata
#### create the variance-covariance matrix
A <- A.mat(GT) # additive relationship matrix

M <- spl2Dmats(x.coord.name = "Col", y.coord.name = "Row", data=DT, nseg =c(14,21))
head(M$data)
# m1g <- mmes(Yield~1+TP.CR.2+TP.CR.3+TP.CR.4,
#             random=~Rowf+Colf+vsm(ism(M$fC))+vsm(ism(M$fR))+
#               vsm(ism(M$fC.R))+vsm(ism(M$C.fR))+vsm(ism(M$fC.fR))+
#               vsm(ism(id),Gu=A),
#             data=M$data, tolpar = 1e-6,
#             iters=30)
# 
# summary(m1g)$varcomp

summary form a GLMM fitted with mmer

Description

summary method for class "mmer".

Usage

## S3 method for class 'mmer'
summary(object, ...)

Arguments

Value

vector of summary

Author(s)

Giovanny Covarrubias-Pazaran

See Also

summary, mmer

summary form a GLMM fitted with mmes

Description

summary method for class "mmes".

Usage

## S3 method for class 'mmes'
summary(object, ...)

Arguments

Value

vector of summary

Author(s)

Giovanny Covarrubias-Pazaran

See Also

summary, mmes

Get Tensor Product Spline Mixed Model Incidence Matrices

Description

tpsmmbwrapper is a wrapper of tpsmmb function from the TPSbits package to avoid version dependencies but if you're using this function for your research please cite the TPSbits package. This function is internally used by the spl2Dmatrices function to get Tensor-Product P-Spline Mixed Model Bits (design matrices) for use with sommer.

Usage

tpsmmbwrapper(
  columncoordinates,
  rowcoordinates,
  data,
  nsegments=NULL,
  minbound=NULL,
  maxbound=NULL,
  degree = c(3, 3),
  penaltyord = c(2, 2),
  nestorder = c(1, 1),
  asreml = "mbf",
  eigenvalues = "include",
  method = "Lee",
  stub = NULL
)

Arguments

Value

List of length 7, 8 or 9 (according to the asreml and eigenvalues parameter settings).

1. data = the input data frame augmented with structures required to fit tensor product splines in asreml-R. This data frame can be used to fit the TPS model.

   Added columns:

   • TP.col, TP.row = column and row coordinates

   • TP.CxR = combined index for use with smooth x smooth term

   • TP.C.n for n=1:(diff.c) = X parts of column spline for use in random model (where diff.c is the order of column differencing)

   • TP.R.n for n=1:(diff.r) = X parts of row spline for use in random model (where diff.r is the order of row differencing)

   • TP.CR.n for n=1:((diff.c*diff.r)) = interaction between the two X parts for use in fixed model. The first variate is a constant term which should be omitted from the model when the constant (1) is present. If all elements are included in the model then the constant term should be omitted, eg. y ~ -1 + TP.CR.1 + TP.CR.2 + TP.CR.3 + TP.CR.4 + other terms...

   • when asreml="grp" or "sepgrp", the spline basis functions are also added into the data frame. Column numbers for each term are given in the grp list structure.

2. mbflist = list that can be used in call to asreml (so long as Z matrix data frames extracted with right names, eg BcZ<stub>.df)

3. BcZ.df = mbf data frame mapping onto smooth part of column spline, last column (labelled TP.col) gives column index

4. BrZ.df = mbf data frame mapping onto smooth part of row spline, last column (labelled TP.row) gives row index

5. BcrZ.df = mbf data frame mapping onto smooth x smooth term, last column (labelled TP.CxR) maps onto col x row combined index

6. dim = list structure, holding dimension values relating to the model:

   1. "diff.c" = order of differencing used in column dimension

   2. "nbc" = number of random basis functions in column dimension

   3. "nbcn" = number of nested random basis functions in column dimension used in smooth x smooth term

   4. "diff.r" = order of differencing used in column dimension

   5. "nbr" = number of random basis functions in column dimension

   6. "nbrn" = number of nested random basis functions in column dimension used in smooth x smooth term

7. trace = list of trace values for ZGZ' for the random TPspline terms, where Z is the design matrix and G is the known diagonal variance matrix derived from eigenvalues. This can be used to rescale the spline design matrix (or equivalently variance components).

8. grp = list structure, only added for settings asreml="grp", asreml="sepgrp" or asreml="own". For asreml="grp", provides column indexes for each of the 5 random components of the 2D splines. For asreml="sepgrp", provides column indexes for each of the X and Z component matrices for the 1D splines, plus the composite smooth x smooth interaction term. For asreml="own", provides column indexes for the composite random model. Dimensions of the components can be derived from the values in the dim item. The Z terms are scaled by the associated eigenvalues when eigenvalues="include", but not when eigenvalues="omit".

9. eigen = list structure, only added for option setting eigenvalues="omit". Holds the diagonal elements of the inverse variance matrix for the terms Xc:Zr (called diagr), Zc:Xr (called diagc) and Zc:Zr (called diagcr).

unstructured indication matrix

Description

unsm creates a square matrix with ones in the diagonals and 2's in the off-diagonals to quickly specify an unstructured constraint in the Gtc argument of the vsm function.

Usage

  unsm(x, reps=NULL)

Arguments

Value

$res

a matrix or a list of matrices with the constraints to be provided in the Gtc argument of the vsm function.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Examples

unsm(3)
unsm(3,2)

unstructured covariance structure

Description

usm creates an unstructured covariance structure for specific levels of the random effect to be used with the mmes solver.

Usage

  usm(x, thetaC, theta)

Arguments

Value

$res

a list with the provided vector and the variance covariance structure expected for the levels of the random effect.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Examples

x <- as.factor(c(1:5,1:5,1:5));x
usm(x)
## how to use the theta and thetaC arguments:
# data(DT_example, package="enhancer")
# DT <- DT_example
# theta <- matrix(9:1,3,3); 
# theta[lower.tri(theta)] <- t(theta)[lower.tri(theta)] 
# theta # initial VCs
# thetaC <- fixm(3); thetaC # fixed VCs
# ans1 <- mmes(Yield~Env,
#              random= ~ vsm( usm(Env,theta = theta,thetaC = thetaC),ism(Name) ),
#              rcov= ~ units, nIters = 1,
#              data=DT)
# summary(ans1)$varcomp

vpredict form of a LMM fitted with mmes

Description

vpredict method for class "mmes".

Post-analysis procedure to calculate linear combinations of variance components. Its intended use is when the variance components are either simple variances or are variances and covariances in an unstructured matrix. The functions covered are linear combinations of the variance components (for example, phenotypic variance), a ratio of two components (for example, heritabilities) and the correlation based on three components (for example, genetic correlation).

The calculations are based on the estimated variance parameters and their variance matrix as represented by the inverse of the Fisher or Average information matrix. Note that this matrix has zero values for fixed variance parameters including those near the parameter space boundary.

The transform is specified with a formula. On the left side of the formula is a name for the transformation. On the right side of the formula is a transformation specified with shortcut names like 'V1', 'V2', etc. The easiest way to identify these shortcut names is to use 'summary(object)$varcomp'. The rows of this object can referred to with shortcuts 'V1', 'V2', etc. See the example below.

Usage

vpredict(object, transform)
## S3 method for class 'mmes'
vpredict(object, transform)

Arguments

Details

The delta method (e.g., Lynch and Walsh 1998, Appendix 1; Ver Hoef 2012) uses a Taylor series expansion to approximate the moments of a function of parameters. Here, a second-order Taylor series expansion is implemented to approximate the standard error for a function of (co)variance parameters. Partial first derivatives of the function are calculated by algorithmic differentiation with deriv.

Though vpredict can calculate standard errors for non-linear functions of (co)variance parameters from a fitted mmes model, it is limited to non-linear functions constructed by mathematical operations such as the arithmetic operators +, -, *, / and ^, and single-variable functions such as exp and log. See deriv for more information.

Value

Author(s)

Giovanny Covarrubias

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Lynch, M. and B. Walsh 1998. Genetics and Analysis of Quantitative Traits. Sinauer Associates, Inc., Sunderland, MA, USA.

Ver Hoef, J.M. 2012. Who invented the delta method? The American Statistician 66:124-127. DOI: 10.1080/00031305.2012.687494

See Also

vpredict, mmes

Examples

####=========================================####
####=========================================####
#### EXAMPLE 1
#### simple example with univariate models
####=========================================####
####=========================================####
# data(DT_cpdata, package="enhancer")
# DT <- DT_cpdata
# GT <- GT_cpdata
# MP <- MP_cpdata
# #### create the variance-covariance matrix 
# A <- A.mat(GT)
# #### look at the data and fit the model
# head(DT)
# mix1 <- mmes(Yield~1,
#               random=~vsm(ism(id),Gu=A), 
#               data=DT)
# summary(mix1)$varcomp
# #### run the vpredict function
# vpredict(mix1, h2 ~ V1 / ( V1 + V2 ) )

variance structure specification

Description

vs DEPRECATED NOW. was the main function to build the variance-covariance structure for the random effects to be fitted in the mmer solver.

Usage

  vs(..., Gu=NULL, Gti=NULL, Gtc=NULL, reorderGu=TRUE, buildGu=TRUE)

Arguments

Details

When providing initial values in the Gti argument the user has to provide scaled variance component values. The user can provide values from a previous model by accessing the sigma_scaled output from an mmer model or if an specific value is desired the user can obtain the scaled value as:

m = x/var(y)

where x is the desired initial value and y is the response variable. You can find an example in the DT_cpdata dataset.

Value

$res

a list with all neccesary elements (incidence matrices, known var-cov structures, unknown covariance structures to be estimated and constraints) to be used in the mmer solver.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Covarrubias-Pazaran G (2018) Software update: Moving the R package sommer to multivariate mixed models for genome-assisted prediction. doi: https://doi.org/10.1101/354639

See Also

The core function of the package: mmer

Examples

data(DT_example, package="enhancer")
DT <- DT_example
A <- A_example

## ============================ ##
## example to without structure
## ============================ ##

mix <- mmer(Yield~Env, 
            random= ~ vs(Name),
            rcov=~ vs(units),
            data=DT)

variance structure specification

Description

vsm is the main function to build the variance-covariance structure for the random effects to be fitted in the mmes solver.

Usage

  vsm(..., Gu=NULL, buildGu=TRUE, meN=1, meTheta=NULL, meThetaC=NULL, 
      sp=FALSE, isFixed=FALSE, verbose=TRUE)

Arguments

Details

...

Value

$res

a list with all neccesary elements (incidence matrices, known var-cov structures, unknown covariance structures to be estimated and constraints) to be used in the mmes solver.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Covarrubias-Pazaran G (2018) Software update: Moving the R package sommer to multivariate mixed models for genome-assisted prediction. doi: https://doi.org/10.1101/354639

See Also

The core function of the package: mmes

Examples

data(DT_example, package="enhancer")
DT <- DT_example
DT=DT[with(DT, order(Env)), ]
A <- A_example

# if using mmes=TRUE remember to provide relationship as inverse in the Gu argument
# Ai <- solve(A + diag(1e-4,ncol(A),ncol(A)))
# Ai <- as(as(as( Ai,  "dMatrix"), "generalMatrix"), "CsparseMatrix")

x <- as.character(unique(DT$Name))
DT <- droplevels(DT[which(!is.na(match(DT$Name, x[1:5]))),])
## ============================ ##
## example without structure
## ============================ ##
ism(DT$Name)
mix <- mmes(Yield~Env,
            random= ~ vsm(ism(Name)),
            rcov=~ units,
            nIters=10,
            data=DT)

## ============================ ##
## example to without structure but
## using covariance among levels in the
## random effect Name
## ============================ ##
mix <- mmes(Yield~Env, 
            random= ~ vsm(ism(Name), Gu=A),
            rcov=~ units,
            nIters=10,
            data=DT)
summary(mix)$varcomp
## ============================ ##
## example to use dsm() structure (DIAGONAL)
## ============================ ##
dsm(DT$Year)
mix <- mmes(Yield~Env,
            random= ~ vsm(dsm(Year),ism(Name)),
            rcov=~ vsm(dsm(Year),ism(units)),
            nIters=10,
            data=DT)
summary(mix)$varcomp
## ============================ ##
## example to use atm() structure (level-specific)
## ============================ ##
# unique(DT$Year)
# mix <- mmes(Yield~Env,
#             random= ~ vsm(atm(Year,c("2011","2012")),ism(Name)),
#             rcov=~ vsm(dsm(Year),ism(units)),
#             data=DT)
## ============================ ##
## example to use usm() structure (UNSTRUCTURED)
## ============================ ##
usm(DT$Year)
mix <- mmes(Yield~Env,
            random= ~ vsm(usm(Year),ism(Name)),
            rcov=~ vsm(dsm(Year),ism(units)),
            nIters = 10,
            data=DT)
## ============================ ##
## example using structure in fixed effect
## (notice the isFixed argument)
## ============================ ##
mix <- mmes(Yield~ vsm(atm(Env,"CA.2011"), ism(Name), isFixed = TRUE),
            rcov=~ units,
            nIters=10,
            data=DT)

variance structure specification

Description

vsr DEPRECATED NOW. was the main function to build the variance-covariance structure for the random effects to be fitted in the mmer solver.

Usage

  vsr(..., Gu=NULL, Gti=NULL, Gtc=NULL, reorderGu=TRUE, buildGu=TRUE)

Arguments

Details

When providing initial values in the Gti argument the user has to provide scaled variance component values. The user can provide values from a previous model by accessing the sigma_scaled output from an mmer model or if an specific value is desired the user can obtain the scaled value as:

m = x/var(y)

where x is the desired initial value and y is the response variable. You can find an example in the DT_cpdata dataset.

Value

$res

a list with all neccesary elements (incidence matrices, known var-cov structures, unknown covariance structures to be estimated and constraints) to be used in the mmer solver.

Author(s)

Giovanny Covarrubias-Pazaran

References

Covarrubias-Pazaran G (2016) Genome assisted prediction of quantitative traits using the R package sommer. PLoS ONE 11(6): doi:10.1371/journal.pone.0156744

Covarrubias-Pazaran G (2018) Software update: Moving the R package sommer to multivariate mixed models for genome-assisted prediction. doi: https://doi.org/10.1101/354639

Examples

data(DT_example, package="enhancer")
DT <- DT_example
A <- A_example

## ============================ ##
## example to without structure
## ============================ ##

mix <- mmer(Yield~Env, 
            random= ~ vsr(Name),
            rcov=~ vsr(units),
            data=DT)